수학 ‘100년 난제’ 풀고 홀연히 사라지다

수학 ‘100년 난제’ 풀고 홀연히 사라지다 우주의 형태와 구조에 관한 ‘푸앵카레 추측’ 수학으로 증명한 페렐만과 수학자들 이야기 한승동 기자 » 수학 ‘100년 난제’ 풀고 홀연히 사라지다 〈100년의 난제 푸앵카레 추측은 어떻게 풀렸을까? - 필즈상을 거부하고 은둔한 기이한 천재수학자 이야기〉 가스가 마사히토 지음·이수경 옮김/살림Math·1만1000원 그리고리 야코블레비치 페렐만(Grigory Yakovlevich Perelman, 1966~ ). 그를 아는 사람이 몇이나 될까. 하지만 30대 나이에 수학계가 100년 동안 풀지 못했던 난제를 해결하고 100만달러(12억~13억원)의 상금 수령을 거부한 수학 천재, 고향인 러시아 상트페테르부르크 서민 아파트촌에 은둔하면서 그곳 숲에서 버섯 따기를 즐기며 늙은 어머니의 몇 푼 안 되는 연금과 저금한 돈으로 가난하게 살아간다는 한 비범한 사나이에 대한 언론 보도를 기억하는 사람은 적지 않을 것이다. 2000년 5월 미국 사설 연구기관인 클레이 수학연구소는 인류가 20세기에 풀지 못한 수학의 난제 7가지를 선정하고 이들 문제를 푸는 사람에게 한 문제당 100만달러씩 주겠다고 발표했다. 이 ‘밀레니엄 현상 문제’는 즉각 세계적인 화제가 됐다. 하지만 이 문제의 존재를 더 널리 알린 것은 6년 뒤에 일어난 한 사건이었다. 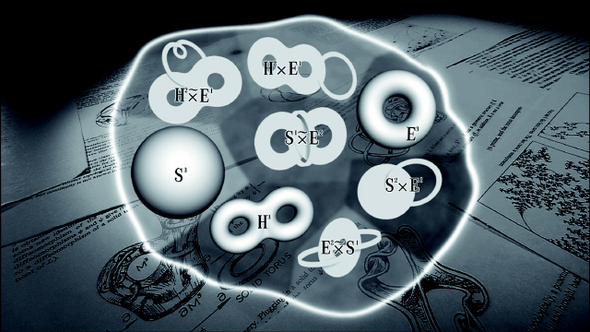» 탁자 위에 놓인 주전자, 접시들을 토폴로지로 분류한 모양. 살림Math 제공 2006년 8월22일 스페인 마드리드에서 국제수학연합(IMU)이 주최한 필즈상 수상식이 열렸다. 수학계 최고의 영예인 필즈상이 그해에 특별히 더 관심을 끈 것은 밀레니엄 현상 문제의 하나인 ‘푸앵카레 추측’을 푼 사람이 수상자가 되리라는 점 때문이었다. 이날 수상자는 모두 4명. 이들 가운데서도 단연 관심이 집중된 사람은 바로 그 문제를 푼 페렐만. 예상대로 ‘100년에 한 번 일어날까 말까 한’ 수학계 대사건을 일으킨 페렐만이 수상자로 호명되고 우레와 같은 박수 소리가 터졌다. 하지만 그는 그곳에 나타나지 않았다. 수상 거부는 70년의 필즈상 역사에서 처음 있는 일이었다. 그해 미국 과학전문지 <사이언스>도 ‘푸앵카레 추측 해결’을 ‘올해의 과학뉴스’ 톱으로 꼽았지만, 일반인들 기억 속에 그 사건은 아마도 거액의 상금에 초연한 채 버섯 따기나 즐기는 가난한 괴짜 수학 천재 이미지로 더 뚜렷하게 남아 있지 않을까? ‘푸앵카레의 추측’이란 건 뭔가? 페렐만은 도대체 어떤 사람인가? 그는 왜 수학자라면 누구나 꿈꾸는 최고의 영예를 거부했을까? 일본 <엔에이치케이>(NHK) 경제·사회정보 프로그램 디렉터 가스가 마사히토의 〈NHK 스페셜〉 팀을 취재길로 떠민 것은 바로 그런 의문이었다. 각국 현장취재를 거쳐 2007년 10월22일 방영된 〈NHK 스페셜〉 제목은 ‘100년의 난제는 어떻게 풀렸나- 천재수학자 실종 수수께끼’. <100년의 난제 푸앵카레 추측은 어떻게 풀렸을까?>는 이를 토대로 삼아 쓴 책이다. 푸앵카레의 추측이란, 프랑스 수학자 앙리 푸앵카레(Henri Poincar<00E9>, 1854~1912)가 1904년에 발표한 논문 ‘위상기하학으로의 제5보족’ 마지막에 “반드시 검토해야 할 문제”라며 붙여 놓은 의문이다. “단일연결인 3차원의 닫힌 다양체는 3차원 구와 위상동형이라고 할 수 있을까?”(지금의 수학 개념으로 요약)

 

 

수학 천재들도 100년 동안 풀지 못한 이 문제를 일반인들은 문제로 인식하기조차 어렵다. 이 책의 장점은 바로 〈NHK〉 일반 시청자들도 이 문제의 정체와 의미를 알아들을 수 있도록 쉬운 예로 설득력 있게 풀어간다는 데 있다. 위상기하학(topology) 전문 수학자 발렌틴 포에나르 파리 오르셰대학 명예교수는 “푸앵카레의 추측은 우주의 형태와 구조에 관한 수학 문제”라며 이런 예를 든다.

누군가 우주의 한 지점에 한 끝을 묶어 놓은 긴 밧줄을 실은 로켓을 타고 우주여행을 떠났다고 상상해보자. 그 사람이 계속 밧줄을 풀어주면서 우주를 한 바퀴 돌고 무사히 지구로 돌아왔다고 칠 때 우주에 빙 두른 밧줄을 잡아당겨 회수할 수 있을까? 단 밧줄 한쪽 끝만 잡아당겨선 안 되고 동시에 처음과 끝 양쪽 모두를 동시에 잡아당겨야 한다. 만일 그렇게 해서 밧줄을 회수할 수 있다면 우주는 둥글다고 할 수 있다.

쉽게 얘기해서, 이게 푸앵카레의 추측이다.

상상이 잘 안되면, 지구를 생각하면 된다. 1519년 마젤란 탐험대가 계속 서진한 끝에 3년 만에 떠난 곳으로 되돌아가 처음 지구를 돌았지만, 그렇다고 해서 지구가 둥근 공처럼 생겼다는 게 증명되는 건 아니다. 만일 지구가 도넛처럼 가운데 구멍이 뚫렸다 해도 마젤란 탐험대는 되돌아올 수 있었을 것이다. 역시 밧줄을 이용한 ‘사고실험’을 통해, 서진한 마젤란의 배가 지구 표면을 빙 두르고 온 밧줄 양끝을 끌어당겨 모두 회수할 수 있다면 지구는 공 모양이다. 만일 도넛 모양이라면 중앙의 구멍 쪽을 통과한 밧줄을 양끝을 잡아당겨 회수할 순 없다.

	» 〈100년의 난제 푸앵카레 추측은 어떻게 풀렸을까?〉

천재 페렐만의 업적은 미분기하학과 물리학을 이용해 푸앵카레의 추측이 ‘참’이라는 걸 수학적으로 처음 증명해낸 것이다. 물론 페렐만 혼자 무에서 만들어낸 건 아니다. 책은 페렐만에 선행한 천재들을 차례로 추적한다. 그리스인 천재 위상기하학자 크리스토스 파파키리아코풀로스, 또다른 수학 난제 ‘4색문제’를 해결한 그의 경쟁자 볼프강 하켄, 고차원 공간에서의 푸앵카레 추측을 입증한 스티븐 스메일, 그리고 “우주가 어떤 형태를 띠든 그것은 반드시 최대 8종류의 서로 다른 단편으로 성립된다”는 ‘기하화 추측’을 도출해낸 윌리엄 서스틴, ‘리치 흐름’(Ricci flow) 방정식을 이용해 기하화 추측과 푸앵카레 추측 증명 가능성을 찾아낸 리처드 해밀턴이 그들이다. 페렐만의 천재성은 그들이 쌓아올린 토대 위에서 비로소 빛날 수 있었다.

푸앵카레는 자신의 추측이 “우리를 아득히 먼 세계로 데려갈 것”이라 했으나 페렐만의 선행자들 대다수가 당도한 곳은 푸앵카레 탄생 3년 전에 나온 허먼 멜빌의 소설 <모비 딕>의 세계였다. 그들은 미친 듯이 거대한 흰고래를 쫓았으나 결국 그 희생물이 되고 말았다.

책은 그러니까 아인슈타인의 일반상대성이론과 양자역학 등 모든 학문으로 이어지는 푸앵카레 추측, 평생을 수학이라는 마력에 끌려 미친 듯 그 모비 딕을 뒤쫓은 수학자들, 그리고 마침내 모비 딕을 잡은 페렐만, 이 세 가지 축을 오가며 진행된다. 다수의 필즈상과 노벨상 수상자를 낸 일본의 저력은, 이처럼 쉽고 매력적인 방법으로 일반 대중에게 그런 일상적이지 않은 세계가 실은 우리 일상과 얼마나 밀접한 연관을 갖고 있는지 끊임없이 그 실상을 보여주고 의미를 되새기게 하는 능력에서 비롯되는 게 아닐까. 한승동 선임기자 sdhan@hani.co.kr

그리고리 페렐만과 수학계 세상은 경악, 학자들은 낙담 » 그리고리 페렐만 클레이 수학연구소가 내건 7개의 밀레니엄 현상 문제는 푸앵카레 추측 외에 P≠NP 추측, 호지(Hodge) 추측, 리만(Riemann) 가설, 양-밀스 방정식(Yang-Mills Existence)과 질량 갭, 나비에-스토크스 방정식(Navier-Stokes Existence and Smoothness), 버치와 스위너턴-다이어(Birch and Swinnerton-Dyer) 추측이 있다. 현대수학과 물리학 최첨단 연구자들로 구성된 과학자문위원회가 ‘오랫동안 해결하지 못한 문제’ ‘최고의 수학자가 씨름해온 전통 있는 문제’ ‘해결할 경우 수학에 지대한 영향을 끼칠 수 있는 문제’를 선정 기준으로 삼아 뽑았다. 푸앵카레 추측을 빼고는 아직 해결된 게 없다. 수학자들이 아니고는 무엇이 문제인지 헤아리기조차 어렵다. 인터넷에 논문 띄우고 ‘필즈상’ 마다한 천재 클레이 수학연구소는 권위 있는 전문지에 실린 뒤 2년간 경과기간을 거쳐 학계에서 받아들여질 수 있는 것으로 확인된 해법에 대해서만 100만달러를 주겠다고 조건을 달았다. 페렐만(사진)의 해법은 2인1조로 된 세 검증팀이 2년여의 검토 끝에 ‘참’이라는 결론을 내렸으나, 연구소가 규정한 수상 자격을 갖추진 못했다. 페렐만은 문제가 나온 2000년께 이미 해법을 발견했으나 2002년 11월, 2003년 3월, 그리고 그해 7월 세 차례에 걸쳐 문제의 논문을 발표했는데, 전문지가 아니라 인터넷에 띄웠으며 자신의 미국 체류기간(1992~95)에 사귀었던 수학자 톈강 매사추세츠공대 교수에게 메일로 그 사실을 알렸다. 그는 애초에 상 타고 상금 받는 데는 전혀 관심이 없었다. 하지만 수학자로서 자신이 이룬 업적은 자랑스러워했고 또 평가받고 싶어했다. 그는 2003년 4월 톈강의 권유로 뉴욕에 가서 거물 수학자들 앞에서 강의했다. 그때 위상기하학자 존 모건은 예상밖으로 미분기하학과 열역학 등 물리학을 응용한 페렐만의 설명을 듣고 충격을 받았다. “그때까지 푸앵카레 추측을 풀기 위해 매달려 온 수학자들은 증명이 모두 끝난 것에 낙담했고, 토폴로지(위상기하학) 수법을 쓰지 않은 것에 낙담했으며, 나아가 증명을 이해하지 못해서 낙담했다. 토폴로지 전문가들은 ‘아, 마침내 푸앵카레 추측이 증명되었다. 하지만 우리는 그 증명을 전혀 이해할 수 없다. 누가 좀 도와줘!’라는 느낌이었다.” 그러나 페렐만은 입증 확인 사실을 알려주는 메일에 답장도 보내지 않고 사라져버렸다. 수학이 인생의 전부였던 이 사나이는 귀국 뒤 근무해오던 상트페테르부르크의 스테클로프 수학연구소도 2005년 12월 갑자기 그만두고 외부와 접촉을 일절 끊었다. 자신의 집 인근의 어머니 집을 오가며 살고 있는 것으로 알려졌다. 〈NHK〉 취재팀은 그의 은사까지 동원해 끈질기게 추적했으나 그와의 접촉에 실패했다. 수학자 타마라 야코브레브나는 페렐만의 유별나 보이는 행동은 급료에서 자신이 직접 가담하지 않은 프로젝트 가산분은 받을 수 없다며 돌려주겠다고 했던 그의 “자신이 정한 행동원칙을 철저히 지키는” 정신에서 비롯된 것이라고 했다. 캐나다의 수학자 존 찰스 필즈가 노벨상엔 없는 수학상을 만들자며 1936년에 만든 필즈상은 4년에 한 번 열리는 국제수학자회의에서 뚜렷한 업적을 쌓은 40살 이하 젊은 수학자들(한 번에 최대 4명까지)을 선정해 수여한다. 수학의 노벨상으로 불리지만 노벨상보다 더 권위가 있다. 한승동 선임기자