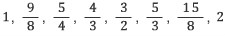|
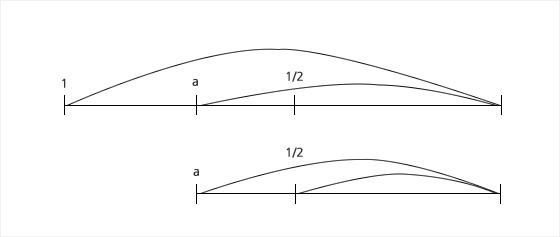
기준 길이 1에 대해 삼분손익법을 적용하여 12음을 구하면, 다음 비를 얻는다.

이 중 짝수 번째, 즉, 삼분손일로 만들어진 것을 6률(陽律)이라 부르고, 홀수 번째, 즉, 삼분익일로 만들어진 것을 6려(陰呂)라 불렀으니, 천자문에도 등장하는 율려조양(律呂調陽)의 ‘율려’가 바로 이것이다. 또한 처음 다섯 음을 궁, 치, 상, 우, 각이라고도 불렀는데 (시대나 나라에 따라 이름이 다른 경우도 있다고 한다) 이를 크기 순으로 늘어놓으면 궁상각치우가 된다. 한편 이 비율(의 역수)은 피타고라스의 음계에도 모두 등장하니, 아름다운 소리를 낸다고 여겼던 비율은 동서양이 따로 없었다고 할 수 있다.
간단한 정수비의 순정률

원칙적으로 정수비로 조율한 것을 모두 순정률이라 부를 수 있지만, 특히 간단한 정수비로 조율한 것만을 순정률(just intonation)이라 부르기도 한다. 실제로 간단한 정수비로 맞출수록 일반적으로는 더 편안한 소리로 들리기 때문이다. 예를 들어 피타고라스는 어울리지 않는 소리로 생각한 5:4 등의 비율(장3도라 부른다)이나 5:3의 비율(장6도)도 실제로 들어보면 협화음정으로 인식되는 경우가 대부분이다. 피타고라스 조율법으로 맞춘 비율 81/64보다 장3도의 비율 5/4가 오히려 어울리게 들린다는 얘기다. 이 두 음정의 차이 1/64을 ‘신토닉 콤마’라 부르는데, 이 차이는 무시하기에는 조금 큰 수준이었다. 따라서 연주자들을 중심으로 피타고라스의 방식을 탈피한 조율법이 모색되었고, 스페인의 수학자 겸 음악 이론가인 라모스(Batolome Ramos de Pareja, 1440~1522)가 고안한 체계가 [실용 음악(Musica practica)]에 남아 있다. 이론적인 음악 이론보다는 실용적인 음악을 위한 체계로 구상된 것인데, 예를 들어 7음계를 아래의 비율로 조율한 것이 대표적인 순정률이다. (물론 12음계를 만드는 방법도 있는데, 여기서는 생략한다.)
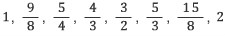
피타고라스 음률의 문제점 : 반음이 다 같은 반음이 아니야

피타고라스 조율법에 의할 경우, 인접한 반음 사이의 비를 보자. 처음 두 수의 비는 a=256/243=1.05349794… 이다. 다음 두 수의 비는 b=(9/8)/(256/243)=2187/2048=1.06787109… 로 a와 다르다. 다행히도(?) 반음은 이 두 종류밖에 나오지 않는다. (참고로 a, b의 곱은 9/8이며, a, b의 비는 피타고라스의 콤마다.) 인접한 반음 사이의 비를 차례로 늘어 쓰면 다음과 같다.
a, b, a, b, a, b, a, a, b, a, b, a
뭔가 규칙성이 흐트러진다는 것이 한눈에도 보일 것이다. 피타고라스의 콤마를 무시하고 타협한 결과 필연적으로 따를 수밖에 없는 현상인데, 특히 협주를 한다거나 조옮김 등을 하려고 할 때 치명적인 불협화음을 수반하는 문제를 낳는다.
무슨 뜻인지 피타고라스 조율법으로 프렛의 간격을 매긴 기타를 예를 들어 설명해 보자. 편의상 요즘 대부분의 기타처럼 6번 현과, 5번 현은 개방현일 때 각각 ‘미’와 ‘라’ 소리를 내도록 조율했다고 하자. 즉, 6번 현의 5번째 프렛을 누르고 낸 소리와, 5번 현의 개방현이 같은 소리를 내도록, 즉 완전4도로 조율했다고 하자는 것이다. 이제 각 현을 한 프렛씩 이동하여 6번 현의 6번째 프렛과, 5번 현의 첫 번째 프렛을 짚은 채 소리를 내면, 같은 소리가 나지 않는다! 미에서 올림 미로는 a배, 라에서 올림 라로는 b배가 되기 때문이다.
순정률의 문제점
사실 이런 문제점은 순정률을 사용하는 한, 즉, 정수 비를 사용하는 한 항상 존재한다. 예를 들어 간단한 정수비를 사용한 순정률에서는 온음의 간격이 10/9과 9/8 두 가지가 혼재하는 문제점이 있는 것이다. 따라서 순정률을 사용할 경우 어떤 화음은 어울리지만, 어울리지 않는 화음이 필연적으로 남게 된다. 일정한 음역대에서 악기 하나만 사용한다면야 문제가 없지만, 조옮김 등을 해야 하거나 두 개 이상의 성부가 들어가는 다성음악 등의 경우, 필연적으로 문제점이 생기는 것이다. 이런 문제점 때문에 오르간이나 하프시코드를 특수 제작하여 연주하는 경우까지 있었다.
순정률이 조화로운 소리를 내기는 하나 이러한 문제점이 있으므로, 대안을 모색하기 시작한 건 당연하다. 특히 16, 17세기부터 한 옥타브를 균등하게 분할하여 반음의 간격을 일정하게 하자는 주장이 꾸준히 나오기 시작하였는데, 사실 수학적으로는 훨씬 이전부터 대두된 문제였다.
|